Sine definition – Embark on an enlightening exploration of the sine function, a cornerstone of trigonometry that unlocks the mysteries of periodic motion and wave phenomena. From its mathematical definition to its myriad applications, prepare to delve into the fascinating world of sine.

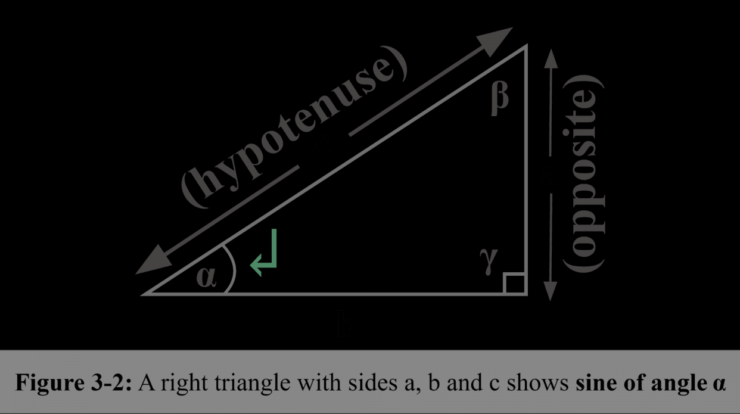
The sine function, meticulously defined as the ratio of the opposite side to the hypotenuse in a right triangle, unveils a profound connection to the unit circle. This relationship forms the bedrock of trigonometry, enabling us to navigate angles and distances with precision.

Definition of Sine: Sine Definition

Sine is a trigonometric function that measures the vertical component of a right triangle. It is defined as the ratio of the length of the opposite side to the length of the hypotenuse.

In a unit circle, the sine of an angle is equal to the y-coordinate of the point where the terminal side of the angle intersects the circle.

Applications of Sine

• Sound waves: Sine waves are used to represent sound waves, as they have a smooth, periodic shape that can be used to model the vibrations of sound.
• Pendulums: The period of a pendulum is proportional to the sine of the angle at which it is released.
• Navigation and surveying: Sine is used to calculate angles and distances in navigation and surveying, such as the distance between two points on a map.

Properties of Sine, Sine definition

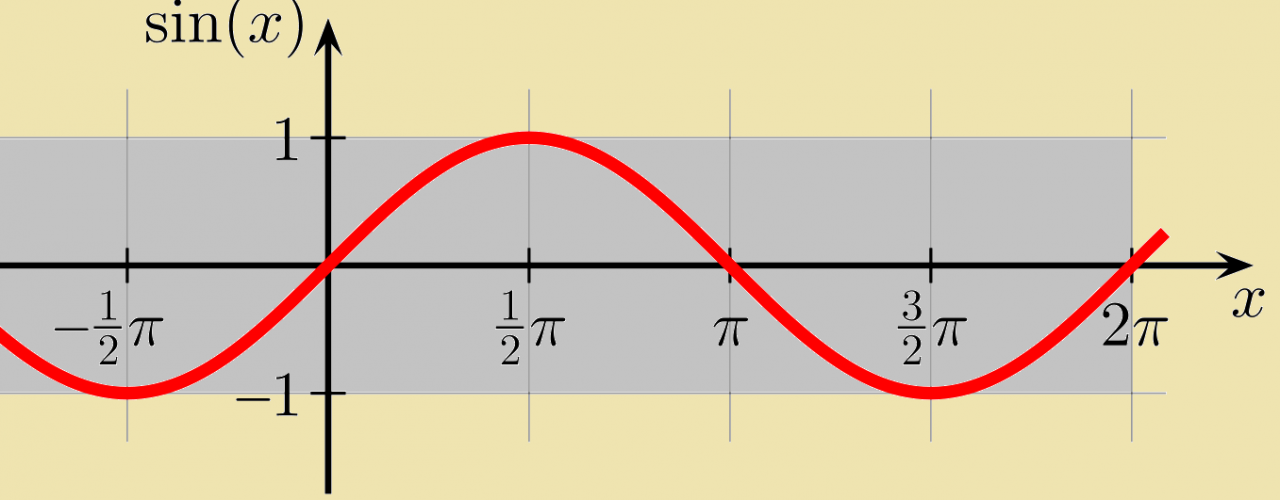
• Periodicity: Sine is a periodic function with a period of 2π.
• Amplitude: The amplitude of sine is 1.
• Range: The range of sine is [-1, 1].

Graphing Sine

The graph of sine is a smooth, periodic curve that oscillates between -1 and 1. The key features of the graph include:

• Intercepts: The sine function intercepts the y-axis at (0, 0) and the x-axis at (π/2, 1) and (3π/2, -1).
• Maximum and minimum values: The sine function has a maximum value of 1 at (π/2, 1) and a minimum value of -1 at (3π/2, -1).

Inverse Sine Function

The inverse sine function, also known as arcsine, is the inverse of the sine function. It is defined as the angle whose sine is a given value.

The inverse sine function is used to find the angle of a pendulum given its period, or to find the angle of a sound wave given its frequency.

History of Sine

The sine function was first discovered by Hipparchus in the 2nd century BC. He used it to calculate the length of the sides of a triangle, and to find the distance to the moon.

The sine function was later developed by Ptolemy in the 2nd century AD. He used it to create a table of sines, which was used by navigators for centuries.

Sine in Different Coordinate Systems

Sine can be defined in different coordinate systems, such as rectangular and polar coordinates.

In rectangular coordinates, sine is defined as the ratio of the y-coordinate to the hypotenuse. In polar coordinates, sine is defined as the ratio of the y-coordinate to the radius.

Conclusion

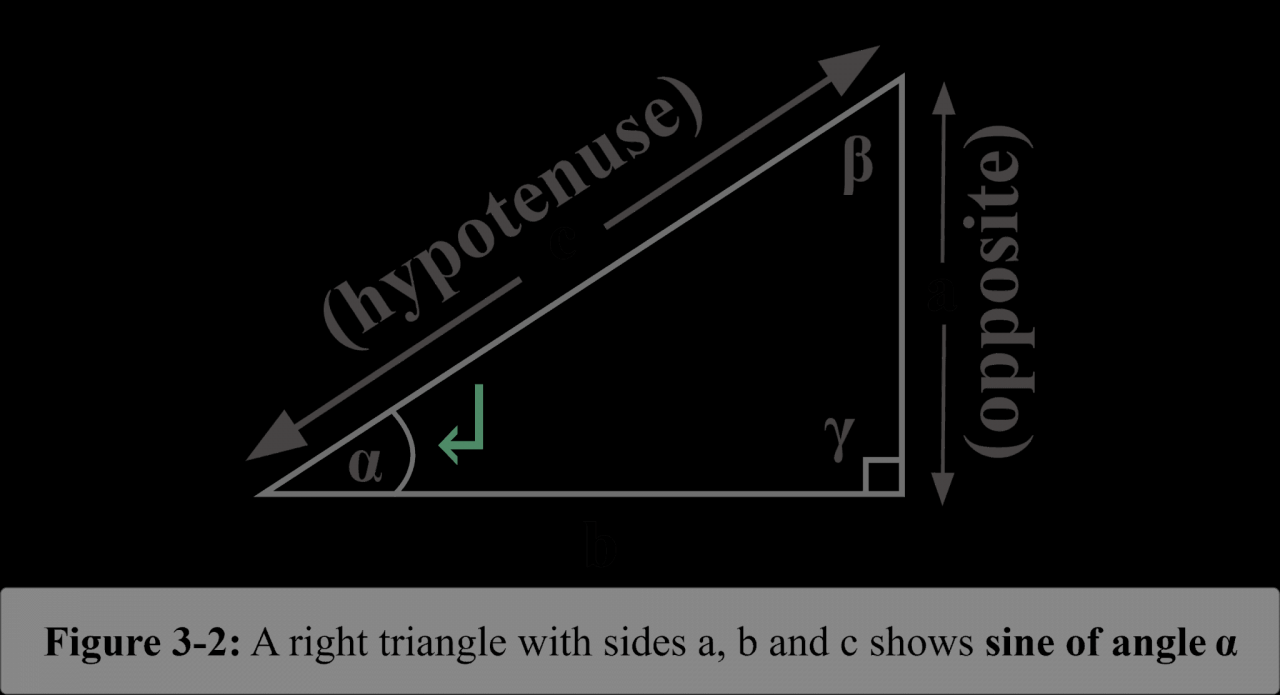
Our exploration of the sine function concludes with a deeper appreciation for its multifaceted nature. Its periodicity, amplitude, and range govern its behavior, shaping the diverse applications we encounter in fields as varied as sound engineering and celestial navigation. Understanding sine empowers us to decipher the rhythmic patterns of the world around us.

Key Questions Answered

What is the mathematical definition of sine?

Sine is defined as the ratio of the opposite side to the hypotenuse in a right triangle.

How is sine related to the unit circle?

The sine of an angle is equal to the y-coordinate of the point on the unit circle that corresponds to that angle.

What are some real-world applications of sine?

Sine is used in a wide variety of applications, including sound waves, pendulums, navigation, and surveying.